Yafei Wang, Guorui Wang*, Xiqi Wu, Jiahao Li, Houbo Li, Xinan Chen, Zhao Zhang, Yuxiang Zhao, Zhong Zhang*
Nano Letters (2025) doi: https://doi.org/10.1021/acs.nanolett.5c04818
ABSTRACT
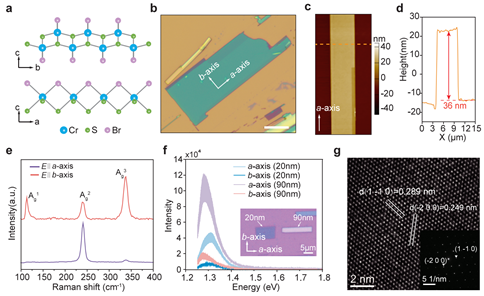
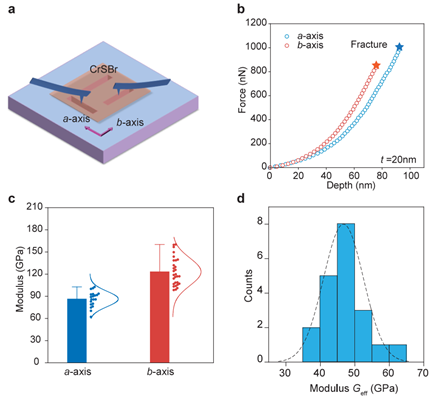
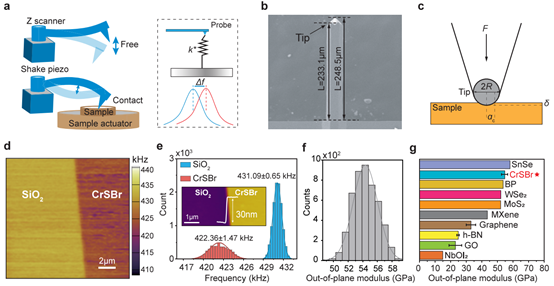
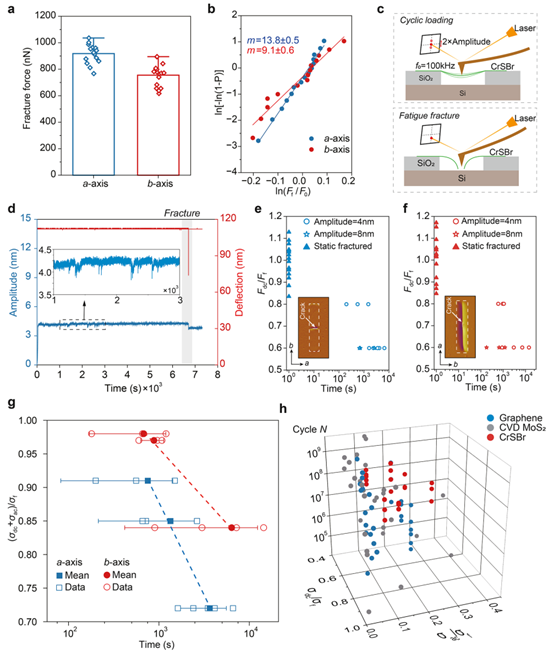
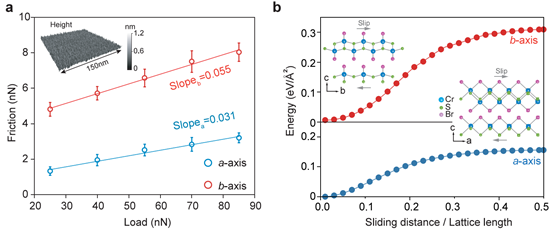
Two-dimensional (2D) materials with intrinsic anisotropy offer unique opportunities for direction-dependent functionality, yet their mechanical anisotropy and long-term reliability remain largely unexplored. Here, we systematically investigate the layered magnetic semiconductor CrSBr, revealing strong in-plane elastic anisotropy (Ea/Eb = 1.43) from angle-resolved atomic force microscopy (AFM) nanoindentation and an out-of-plane modulus of ∼54 GPa from contact resonance AFM, indicative of robust interlayer coupling. Dynamic AFM loading demonstrates pronounced anisotropic fatigue, with superior endurance along the b-axis attributed to enhanced interlayer energy dissipation, consistent with friction measurements and first-principles calculations of interlayer sliding energy. Remarkably, despite its lower fracture strength, CrSBr exhibits fatigue lifetimes comparable to graphene and CVD-grown MoS2 under normalized stress. These results establish CrSBr as a mechanically robust 2D magnetic semiconductor, where anisotropic bonding and interlayer coupling combined govern cyclic damage resistance.

 当前位置:
当前位置: