当前位置:
首页 >
新闻
当前位置:
首页 >
新闻
 当前位置:
首页 >
新闻
当前位置:
首页 >
新闻
微纳米复合材料研究所在探究粘附材料动态粘附方面取得重要进展
研究背景
聚合物粘附材料能与各种材料的基底产生范德华力,在生物工程,传感器等领域有重要应用。过去几十年,人们对粘附材料的粘附性能进行了广泛研究,特别是在动态粘附领域,拉拔速度对粘附性能有显著影响。评价粘附性能的参数主要分为两类:力指标(如拉脱力和粘附功)和持粘指标(如分层时间和粘附冲量)。在粘性材料领域,拉脱力随拉拔速度的变化会导致其他相关粘附参数的变化。目前主流的粘性材料设计和应用主要考虑拉脱力和粘附功,但在无重力空间环境等条件下,粘附冲量更值得关注。
研究简介
近期,中国科学技术大学微纳米复合材料研究所张忠教授团队,在研究粘附材料动态粘附方面,提出了一种新的理论框架。研究旨在系统地探究不同截面的弹性体在动态粘附过程中的粘附参数响应,重点关注四个关键性能参数:拉脱力、粘附功、分层时间和粘附冲量。通过提出力位移曲线的相似性假设,建立了这些粘附参数与拉拔速度之间的幂率关系,阐明了它们的动态响应特性,并通过实验验证了理论的可行性和普适性。研究使用聚二甲基硅氧烷(PDMS)弹性体样品和玻璃基底进行分层实验。实验中,PDMS弹性体样品在不同拉拔速度下从玻璃基底上分层,通过分析力-时间曲线和力-位移曲线,得到了拉脱力、分层时间、粘附冲量和粘附功等参数。研究结果表明四种粘附性能参数与拉拔速度都满足幂率关系,拉脱力和粘附功随拉拔速度的增加而增大,而分层时间和粘附冲量则随拉伸速度的增加而减小。这表明在动态条件下,力指标和持粘指标之间存在竞争关系。之后基于粘附冲量与拉拔速度的幂率关系,估计了无重力环境下粘附机械爪碰撞捕获目标物体的最大允许速度。本研究为优化粘性材料在动态条件下的应用策略和工程设计提供了理论支持,同时为无重力环境下碰撞粘附的最大速度预测提供了理论依据,对空间捕获技术等领域具有重要意义。相关研究以”Dynamic adhesion response of elastomers with square and circular cross-sections”为题,发表在固体力学领域著名期刊Engineering Fracture Mechanics上。

研究内容
本研究首先从实验出发,对于不同厚度、不同截面形状(圆形和方形)的PDMS弹性体样品,在不同拉拔速度vpull下进行分层实验,如图1所示获取其力-位移曲线和力-时间曲线,定义并测量了拉脱力Pc、分层时间Tc、粘附冲量Iad和粘附功Wad这四个粘附性能参数。Gent-Schulz定律作为唯象模型广泛用于动态粘附分析,认为在分层过程中裂纹尖端处发生显著能量耗散,而弹性体其他部分的能量耗散可以忽略不计。所以粘附材料整体依然可以视为线弹性体,从而在粘附力达到拉脱极限前,弹性体伸长量δ正比于粘附力P,且力位移曲线斜率不随拉拔速度增大而增大。所以对于同一样品,如图2所示,其不同拉拔速度下的下的负力值部分的力位移曲线是相似的。

图1. 粘附力测试获取力位移曲线和力时间曲线,并定义四个粘附性能参数

图2. 相同样品不同拉拔速度下力位移曲线具有相似性
根据相似性假设,可以分析得到如下关系:由于粘附功Wad是力位移曲线的积分,故Wad与拉脱力Pc有如下关系式:

随着拉拔速度vpull的增大,脱附时间Tc减小,即Tc正比于完全脱附时的位移除以vpull。又考虑位移和Pc的线性关系于是可得:

粘附冲量Iad为力时间曲线的积分,所以有如下关系:

即基于不同拉拔速度下的力位移曲线的相似性假设,参数Wad,Tc和Iad随vpull的变化可以直接由Pc随vpull的变化推导出来。参考Li等人得到的拉脱力Pc与拉拔速度vpull的幂率关系:

可以得到其它粘附参数与vpull的关系:

其中n来源于Gent-Schulz定律中裂纹扩展速率的指数,即:

其中vp是裂纹扩展速率,γ是界面能,w是单位面积粘附功,vn和n是材料粘性相关参数,实验得到n = 0.713。图3详细展示了在实验过程中,拉脱力Pc、粘附功Wad、粘附时间Tc和粘附冲量Iad这四个粘附性能参数随拉拔速度vpull变化的具体情况。在图3中对比实验指数和理论幂率关系的指数,证明了上述参数Pc,Wad,Tc和Iad随vpull的幂率关系公式的准确性。

图3. 四种粘附参数的实验与理论动态粘附响应对比
无约束粘附的典型工况考虑的是处于空间环境中的粘附抓手与目标物体之间的粘附行为,此时抓手与目标物体没有其他的固定约束。因此,当粘附抓手需要对目标物体进行粘附捕获时,通常需要通过一定的速度碰撞来实现粘附过程,如图4所示。然而,这一过程中如果碰撞时的相对速度过高,粘附抓手将难以实现对目标物体的有效捕获,甚至可能因为冲击力过大而导致与目标物体分离。如图4(b)所示,碰撞将导致粘附爪以相对速度vout与目标物体分离。注意相对分离速度为vout时,弹性体粘附材料恰好处于不受力状态,粘附材料厚度为初始厚度。由于碰撞时动能损失,设Rvvin = vout,其中Rv的值在0到1之间。根据Iad与vpull的幂律关系,碰撞粘附允许的最大速度vin(max)满足:

其中m*是粘附爪与目标物体的约化质量,nI = (n-2)/(2+n)。则对于使用相同的弹性体粘附材料的粘附抓手,vin(max)与m*之间也存在上式的幂率关系,且更大m*的会导致vin(max)的减少。

图4.粘附爪通过碰撞捕获目标物体的过程
中国科学技术大学辜萍副教授为论文的通讯作者,中国科学技术大学博后陈子健为论文的第一作者。该工作得到了国家重点研发计划和国家自然科学基金等基金项目的资助。
原文链接:
https://doi.org/10.1016/j.engfracmech.2025.111508
- 返回列表
-
项目中期2025年11月14日国家重点研发计划“用于极端环境防护的结构功能一体化纳米复合材料及应用探索”项目中期评估会议在常州召开11月10日上午,中国科学技术大学张忠教授牵头承担的国家重点研发计划“纳米前沿”重点专项“用于极端环境防护的结构功能一体化纳米复合材料及应用探索”项目中期总结暨课题评议交流会在常州召开。 项目中期评估会议由项目负责人张忠教授主持。会议邀请了由中国科学院过程工程研究所陈运法研究员担任组长的专家组进行咨询与评估。专家组成员包括南方科技大学叶林院士、中国科...了解更多

-
启动会2023年11月21日国家重点研发计划“纳米前沿”重点专项项目启动暨实施方案论证会在北京成功召开11月17日上午,由中国科学技术大学牵头,联合国家纳米科学中心、清华大学、航空工业济南特种结构研究所、合肥航太电物理技术有限公司、上海飞机制造有限公司等六家单位共同承担的“十四五”国家重点研发计划 “纳米前沿”重点专项项目启动暨实施方案论证 会在北京召开。项目瞄准空天领域防雷击、防高能冲击及防覆冰的重大需求,发展系列碳纳米复合防护材料和技术,实现极致的结构功能一体化性能,满足新一代防护材料极端服役环境要...了解更多

-
2025年09月12日中国科大联合国家纳米中心合作研发纳米复合超黑材料 持续助力卫星高精度空间探测9月5日,我国在西昌卫星中心使用长征三号丙运载火箭/远征一号上面级,成功将试验二十九号卫星发射升空。该卫星主要用于空间环境探测及相关技术试验。中国科学技术大学工程科学学院微纳米复合材料研究所和国家纳米科学中心纳米复合材料团队联合为该卫星的多个光学构件表面(包括复杂异型遮光罩、柔性可展开结构、精密光学支撑结构及热控薄膜等)研发制备了大面积纳米复合超黑材料,将大幅提升卫星空间环境探测能力。纳米复合超黑材...了解更多

-
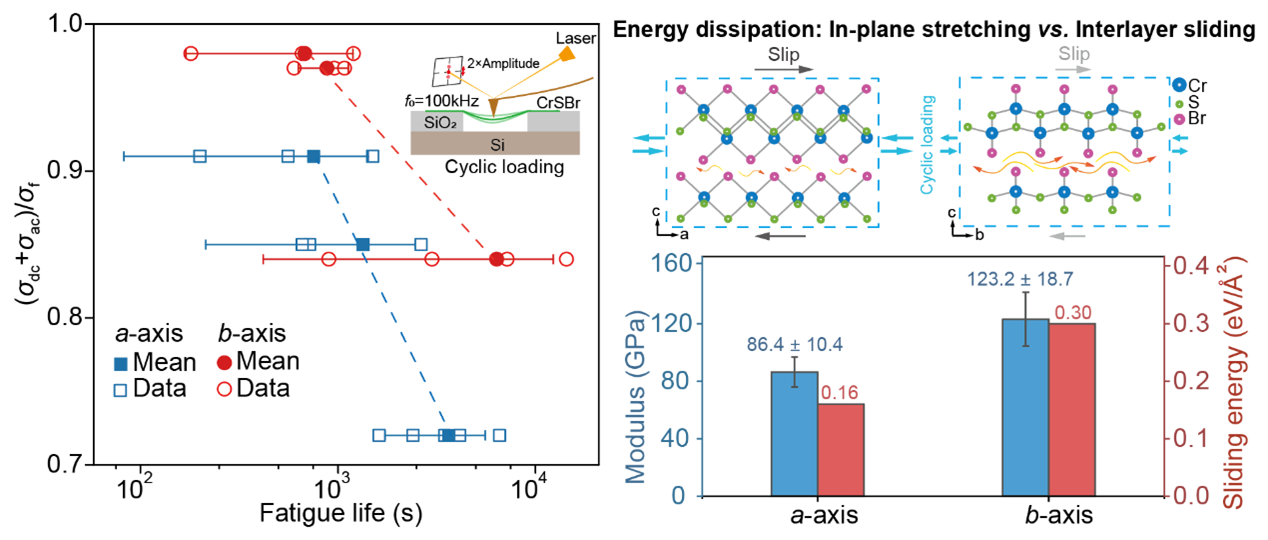
研究进展2025年11月11日微纳米复合材料研究所在二维磁性半导体各向异性力学与疲劳性能研究中取得新进展研究背景二维材料的各向异性力学特性近年来受到广泛关注。以往研究多聚焦于面内晶格结构的方向依赖性,探讨其对弹性模量、断裂强度与韧性的影响。其中,弹性性能决定了应变调控的可调范围,强度与韧性则不仅影响二维晶体的剥离与加工过程,也直接决定其损伤演化与器件服役寿命。在单层二维晶体中,面内晶格取向的不对称性是力学各向异性的主要来源。不同于石墨烯的六方晶格结构,黑磷、黑砷、MoO3、As2S3等低对称性材料中,键合网...了解更多