当前位置:
首页 >
新闻
当前位置:
首页 >
新闻
 当前位置:
首页 >
新闻
当前位置:
首页 >
新闻
微纳米复合材料研究所在描述随机粗糙表面动态粘附方面取得进展
研究背景
近几十年来,干粘附材料的粘附性能得到了广泛研究。由聚合物制成的干粘附材料,能够与各种材质的基板产生强粘附,有望应用于机械爪、仿壁虎机器人等领域。然而,粘附材料的实际应用中,基板表面的粗糙度以及动态粘附行为对粘附性能有显著影响。粗糙表面会降低实际接触面积,导致粘附性能下降;而动态粘附过程中,拉拔速度的增加会使粘附材料拉脱力增大,反映出非准静态的粘附特性。目前,如何综合考虑粗糙表面和动态粘附对粘附性能的影响仍然是一个挑战。
研究简介
本研究旨在开发一个综合模型,用于描述聚合物粘附材料在粗糙基板上的动态粘附行为,特别是拉拔速度对拉脱应力的影响。研究结合了Greenwood-Williamson(GW)模型和Muller动态粘附理论,并考虑将拉拔速度和界面分离速度解耦,提出了一个数值方法来模拟弹性体与粗糙基板之间的动态分离过程,并通过实验结果验证了模型的准确性。相关研究成果以“Normal dynamic adhesion of an infinite elastomer layer on a statistically rough substrate”为题,发表在力学学科Top期刊《Journal of the Mechanics and Physics of Solids》。
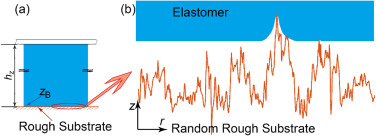
图1. 弹性体与粗糙基板接触示意图(a) 厚度为hz的无限大弹性体膜与无限大刚性粗糙基板接触示意图 (b) 粗糙基板与弹性体底面的接触示意图
研究内容
使用GW模型描述随机粗糙表面,GW模型将随机粗糙表面简化为大量独立的抛物面凸起,从而将复杂的粗糙表面接触问题转化为基于单个凸起接触的统计问题。粗糙表面与弹性体的作用是所有独立凸起与弹性体的作用之和。引入Muller模型描述单个抛物面凸起的动态粘附行为。Muller模型基于Gent-Schulz定律对JKR模型进行了修正,从而可以描述单个抛物面凸起与半空间弹性体分层时拉拔速率对拉脱力和粘附功的动态影响。结合GW模型和Muller模型实现对界面动态行为的描述。
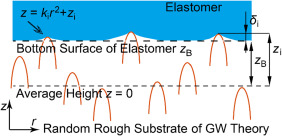
图2. 弹性体底面与GW粗糙基板之间的接触
进一步考虑到当弹性体上表面以固定拉拔速度分离时,弹性体将发生形变和拉伸,导致界面分离速度的实时变化。结合界面动态行为,建立了无限大弹性体膜从无限大随机粗糙基板上法向分层的动态粘附模型。为了计算拉拔速度vU固定时变化的界面分离速度vB,本研究认为真实的vB必须满足弹性体应力等于界面应力,并使用分析步方法进行数值求解。粗糙表面动态粘附模型能较好地再现弹性体与粗糙基板接触时的拉伸回弹现象。
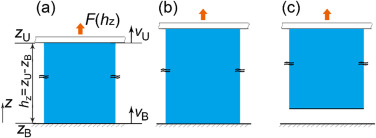
图3. 弹性体分离过程中的拉伸和回弹阶段 (a)弹性体表面施加恒定拉拔速度 (b)弹性体被拉伸 (c)弹性体分离过程的回弹
基于粗糙表面动态粘附模型分析了不同弹性体模量(49.4~4000 kPa)和基板粗糙度(10⁻⁴~10⁻⁷ m)下,粘附应力σpull-off与拉拔速度vU的幂函数关系,即σ_(pull-off)∝v_U^(k_exp )。理论得到幂函数的指数kexp值与基板粗糙度zrough和弹性体模量E有关,zrough - E空间中存在分割线:20×(zrough/zk) = (E/Ek)-0.354,这里zk = 1 mm,Ek = 1 kPa。当20×(zrough/zk) < (E/Ek)-0.354时,kexp相对稳定,粘附应力满足σpull-off ∝ vU0.250。当20×(zrough/zk) > (E/Ek)-0.354时,kexp急剧增大。这是由于粗糙基板接触弹性体的凸起的压入深度分布影响该幂函数的指数kexp。实验结果也认可了分割线20×(zrough/zk) = (E/Ek)-0.354对kexp稳定区和骤增区的划分。本研究理论简化了弹性体与粗糙基板接触粘附时拉拔速度vU对粘附应力σpull-off的影响,为粘附弹性体面对粗糙基板接触场景的设计提供了重要的理论依据。
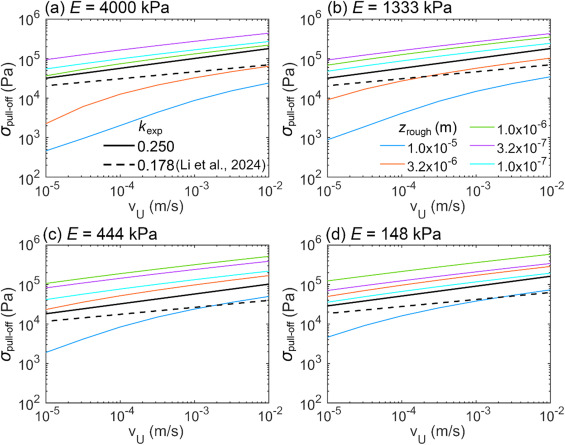
图4.对数坐标下w对σpull-off的影响
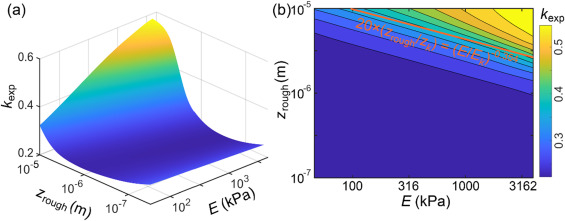
图5. 粗糙表面动态粘附模型得到的kexp与zrough和E的关系 (a)kexp的三维分步示意图 (b)zrough-E平面上区分kexp稳定区与骤增区的分界线
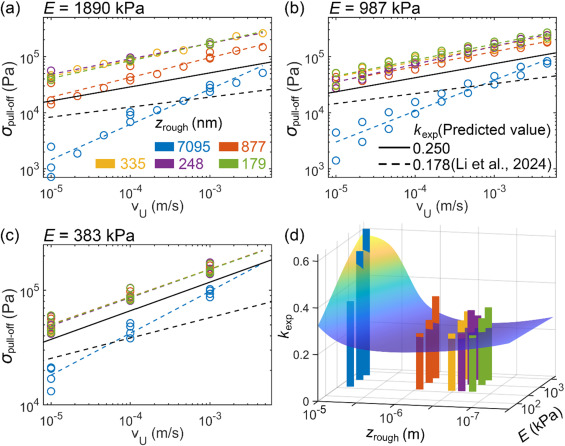
图6. 不同zrough和E下w对σpull-off的实验结果 (a~c)不同样品模量的σpull-off-w图 (d)zrough-E空间中实验kexp结果与理论kexp结果的比较
中国科学技术大学近代力学系博士生陈子健为第一作者,赵旸教授、辜萍副教授为共同通讯作者。中国科学技术大学张忠教授和汪国睿教授为本工作提供了指导性建议。该工作得到了科技部国家重点研发计划、国家自然科学基金委员会项目资助。
原文链接:
- 返回列表
-
启动会2023年11月21日国家重点研发计划“纳米前沿”重点专项项目启动暨实施方案论证会在北京成功召开11月17日上午,由中国科学技术大学牵头,联合国家纳米科学中心、清华大学、航空工业济南特种结构研究所、合肥航太电物理技术有限公司、上海飞机制造有限公司等六家单位共同承担的“十四五”国家重点研发计划 “纳米前沿”重点专项项目启动暨实施方案论证 会在北京召开。项目瞄准空天领域防雷击、防高能冲击及防覆冰的重大需求,发展系列碳纳米复合防护材料和技术,实现极致的结构功能一体化性能,满足新一代防护材料极端服役环境要...了解更多

-
研究进展2025年04月10日微纳米复合材料研究所在描述粘附材料界面应力和脱附行为研究中取得重要进展研究背景受壁虎脚掌强粘附力启发,近年来研究者们致力于开发人工干粘附材料,这些材料具有可重复使用、多功能和轻质等特点,能够在不同基底上产生超过可观粘附力,有望广泛应用于仿壁虎机器人和多功能机械爪等领域。为了提升这些粘附材料的性能,当前研究聚焦于粘附机制和粘附力控制方面。粘附机制研究的关键是探索影响界面应力和脱附行为的关键因素,并期望量化拉脱力。而粘附力的控制则依赖于利用粘附机制来设计先进粘附系统,例...了解更多

-
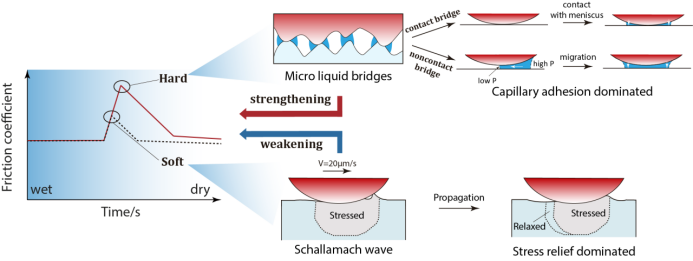
研究进展2025年02月28日微纳米复合材料研究所在软材料界面Schallamach波对毛细粘附摩擦增强影响研究中取得新进展研究背景软材料接触界面广泛存在于各种实际应用中,例如生物胶粘剂,汽车轮胎和关节软骨。实际上,软材料接触界面往往由于冷凝水或有机污染而处于(部分)润湿状态,这可能会对摩擦造成不利影响,导致车辆打滑或橡胶磨损等。因此,研究橡胶的润湿摩擦特性,对提高系统的使用性能,确保设备运行可靠性具有重要意义。软材料摩擦与其他刚性体(如金属或陶瓷)有很大不同,其中软接触界面不仅增强了黏附力,而且还受到弹性滞后贡献的影...了解更多
-
研究进展2025年02月27日微纳米复合材料研究所在描述随机粗糙表面动态粘附方面取得进展研究背景近几十年来,干粘附材料的粘附性能得到了广泛研究。由聚合物制成的干粘附材料,能够与各种材质的基板产生强粘附,有望应用于机械爪、仿壁虎机器人等领域。然而,粘附材料的实际应用中,基板表面的粗糙度以及动态粘附行为对粘附性能有显著影响。粗糙表面会降低实际接触面积,导致粘附性能下降;而动态粘附过程中,拉拔速度的增加会使粘附材料拉脱力增大,反映出非准静态的粘附特性。目前,如何综合考虑粗糙表面和动态粘附对...了解更多